US Equities Clearing Price Examples

Introduction

OneChronos periodic auctions run throughout the trading day, ~10x per second. Instead of matching orders one by one using price-time priority, we use mathematical optimization to seek optimal matches across all orders for all securities within an auction.

Each auction looks for the configuration of potential order matches and per-security clearing prices that will result in the most price improvement dollars cleared within the auction. Price improvement dollars refers to the difference between the limit price on an order and the auction clearing price (i.e., the price at which an order fills), times the quantity filled.

The following examples illustrate the OneChronos order matching process. They are non-exhaustive, demonstrating general and simple outcomes in which the OneChronos optimizer finds the optimal outcome. Our Form ATS-N details the process, and you can always reach us at [email protected].

Example 1

Example 1: Scenario

• Order 1: Buy 100 @ $10.01
• Order 2: Sell 100 @ $10.00

Example 1: Outcome

Orders 1 and 2 fill 100 shares @ $10.005.

Example 1: Key Takeaways

Any price in the interval $[\$10.000000, \$10.010000]$ is a valid clearing price. In the absence of other constraints, OneChronos fills at the midpoint of the clearing price range.

Example 2

Example 2: Scenario

• Order 1: Buy 100 @ $10.01
• Order 2: Buy 100 @ $10.01
• Order 3: Sell 200 @ $10.00

Example 2: Outcome

Orders 1 and 2 buy 100 shares @ $10.005. Order 3 sells 200 shares @ $10.005.

Example 2: Key Takeaways

Within an auction, all orders for a specific trading symbol will fill at a uniform price. If there is no imbalance, all orders will fill in their entirety.

Example 3

Example 3: Scenario

• Order 1: Buy 100 @ $10.01
• Order 2: Buy 100 @ $10.01
• Order 3: Sell 100 @ $10.00

Example 3: Outcome

Orders 1 and 2 have a 50/50 chance of receiving a fill for 100 shares @ $10.005. Order 3 fills 100 shares @ $10.005.

Example 3: Key Takeaways

If there is an imbalance where two or more orders contribute the same number of price improvement dollars (Orders 1 and 2) and are the same size, allocation is round-robin from a randomized starting point.

Example 4

Example 4: Scenario

• Order 1: Buy 100 @ $10.02
• Order 2: Buy 100 @ $10.01
• Order 3: Sell 100 @ $10.00

Example 4: Outcome

Orders 1 and 3 receive a fill for 100 shares @ $10.01.

Example 4: Key Takeaways

Order 1 has a higher match priority than Order 2 given that it contributes more price improvement dollars to the auction: $100\cdot(10.02-10.01) > 100\cdot(10.01-10.01)$.

Example 5

Example 5: Scenario

• Order 1: Buy 100 @ $10.01
• Order 2: Buy 200 @ $10.01
• Order 3: Sell 200 @ $10.00

Example 5: Outcome

Order 2 receives a fill for 200 shares @ $10.005. Order 3 receives a fill for 200 shares @ $10.005.

Example 5: Key Takeaways

Like Example 3, partially filling Orders 1 and 2 would result in the same notional price improvement and volume as filling 200 shares of Order 2. However, filling Order 2 in its entirety maximizes the average fill size:

$$\begin{aligned} \frac{200+200}{2} &\geq \frac{o_1+o_2+200}{3} \\ o_1 &\in [0, 100] \\ o_2 &\in [0, 200] \\ o_1+o_2 &= 200 \end{aligned}$$

Example 6

Example 6: Scenario

• Order 1: Buy 100 @ $10.02
• Order 2: Buy 100 @ $10.04
• Order 3: Sell 100 @ $10.01
• Order 4: Sell 100 @ $10.02

Example 6: Outcome

Orders 1–4 fill 100 shares @ $10.02.

Example 6: Key Takeaways

Filling all orders is both possible and optimal, and the only price at which all orders can fill is $10.02. Neither the least aggressive buy (Order 1) nor the least aggressive sell (Order 4) receives price improvement; Orders 2 and 3 do.

NOTE: Examples 7 through 10 use hypothetical Expressive Bidding functionality, to illustrate the general approach involved in solving a combinatorial auction such that aggregate price improvement is maximized.

Note that Expressive Bidding is currently enabled for "Pairs" only (i.e. Expressive Orders consisting of two symbols). For more information, please see our Form ATS-N.

Example 7

Example 7: Scenario

• Order 1: Buy 200 all-or-nothing @ $10.01 (Expressive Bidding constraint)
• Order 2: Buy 100 @ $10.02
• Order 3: Sell 200 @ $10.00

Example 7: Outcome

Orders 1 and 3 fill 200 @ $10.005.

Example 7: Key Takeaways

Order 1 is a simple Expressive Bid. Expressive Bids allow Users to express complements and substitutes and control execution risk. Order 1 is an Expressive Bid that ensures that the order fills in entirety or not at all; examples involving more sophisticated Expressive Bids will follow.

Matching Order 1 against Order 3 yields the same price improvement dollars as matching Order 2 against Order 3: $200(10.01-10.00) = 2.00 = 100(10.02-10.00)$. However, matching Order 1 against Order 3 also maximizes liquidity (trade volume), which is the optimization's secondary objective. The clearing price range given the match is $[\$10.00,\ \$10.01]$, so $10.005 is the midpoint.

Example 8

Example 8: Scenario

• Order 1: Buy 100 ABC @ 10.01 EXCLUSIVE OR Buy 100 XYZ @ 11.00 (Expressive Bidding constraint)
• Order 2: Buy 100 XYZ @ 11.00
• Order 3: Sell 100 ABC @ 10.00
• Order 4: Sell 100 XYZ @ 10.98

Example 8: Outcome

Orders 1 and 2 have a 50/50 chance of filling 100 XYZ @ 10.99; Order 4 fills @ 10.99. Order 3 does not receive a fill.

Example 8: Key Takeaways

Expressive Bids are neither advantaged or disadvantaged with respect to match priority, but their ability to express substitutability benefits limit orders and other Expressive Bids alike. If Order 1 fills, the optimizer will choose the XYZ leg, given that it yields more price improvement dollars to the auction than the ABC leg.

Example 9

Example 9: Scenario

• Order 1: Buy 100 ABC AND Sell 100 XYZ at a spread of $0.05 or better (Expressive Bidding constraint)
• Order 2: Sell 100 ABC @ $10.00
• Order 3: Buy 100 XYZ @ $10.08

Example 9: Outcome

Order 1 fills 100 ABC @ $10.015 and 100 XYZ @ $10.065 resulting in a spread of $0.05. Order 2 fills @ $10.015. Order 3 fills @ $10.065.

Example 9: Key Takeaways

A system of inequalities dictates the clearing price range for ABC and XYZ:

$$\begin{aligned} p_\textrm{xyz} - p_\textrm{abc} &\geq 0.05 \\ p_\textrm{abc} &\geq 10.00 \\ p_\textrm{xyz} &\leq 10.08. \end{aligned}$$

These inequalities form a triangle with vertices $(p_\textrm{xyz}, p_\textrm{abc})$ at $(10.05, 10.00)$, $(10.08, 10.00)$, and $(10.08, 10.03)$.

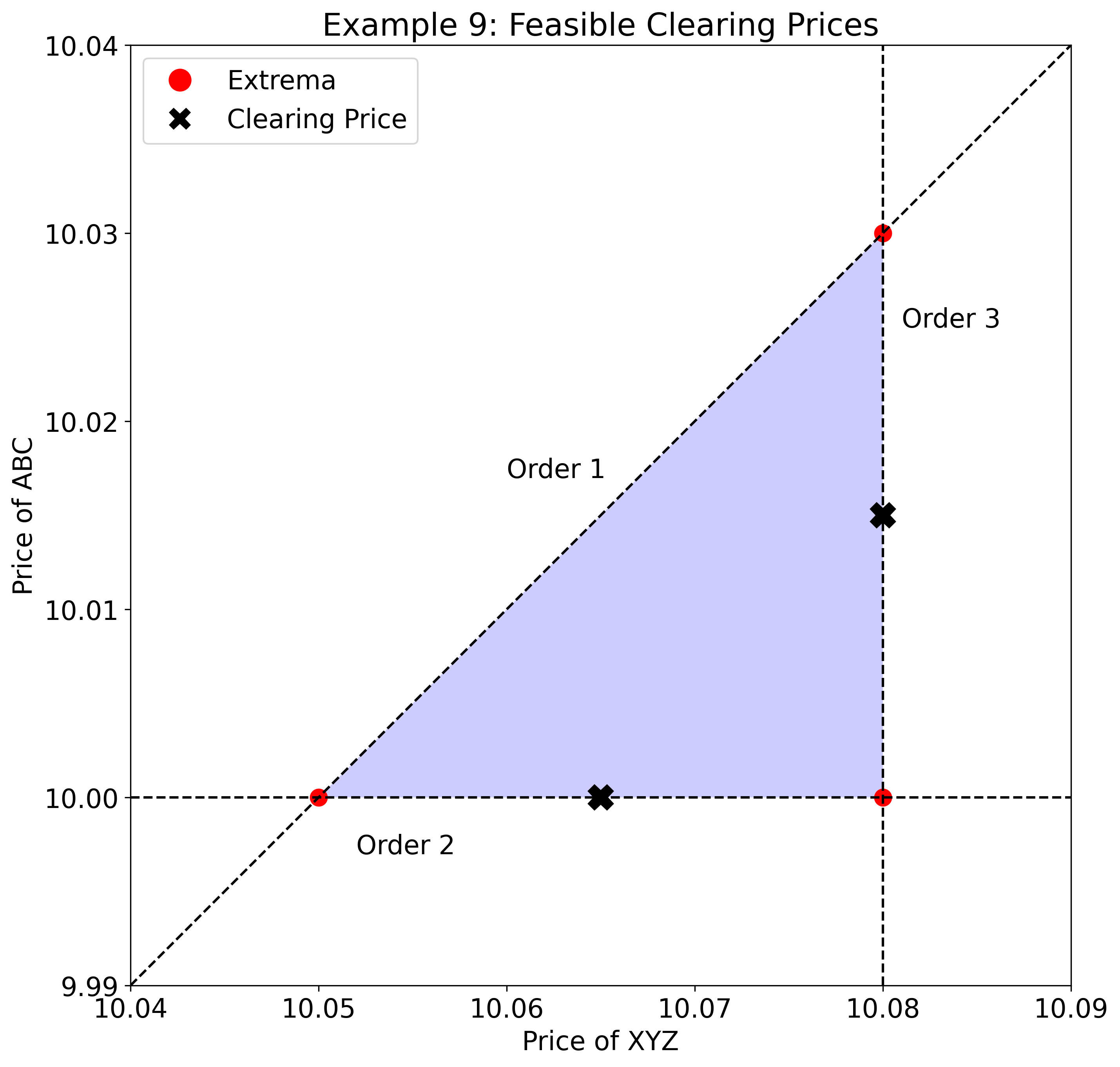
Thus, the clearing price range for $p_\textrm{xyz}$ is $[\$10.05,\, \$10.08]$ and the midpoint is $10.065. Similarly, the clearing price range for $p_\textrm{abc}$ is $[\$10.00,\, \$10.03]$ and the midpoint is $10.015.

In this scenario, Orders 2 and 3 receive $0.015/share price improvement, and Order 1 trades at its threshold spread. In this scenario, the auction dynamics resulted in Order 1 receiving no price improvement and Orders 2 and 3 "splitting the difference." The following example shows that this is not always the case. Both Expressive Bids and unconstrained (e.g., limit) orders are eligible for and receive price improvement in the same way.

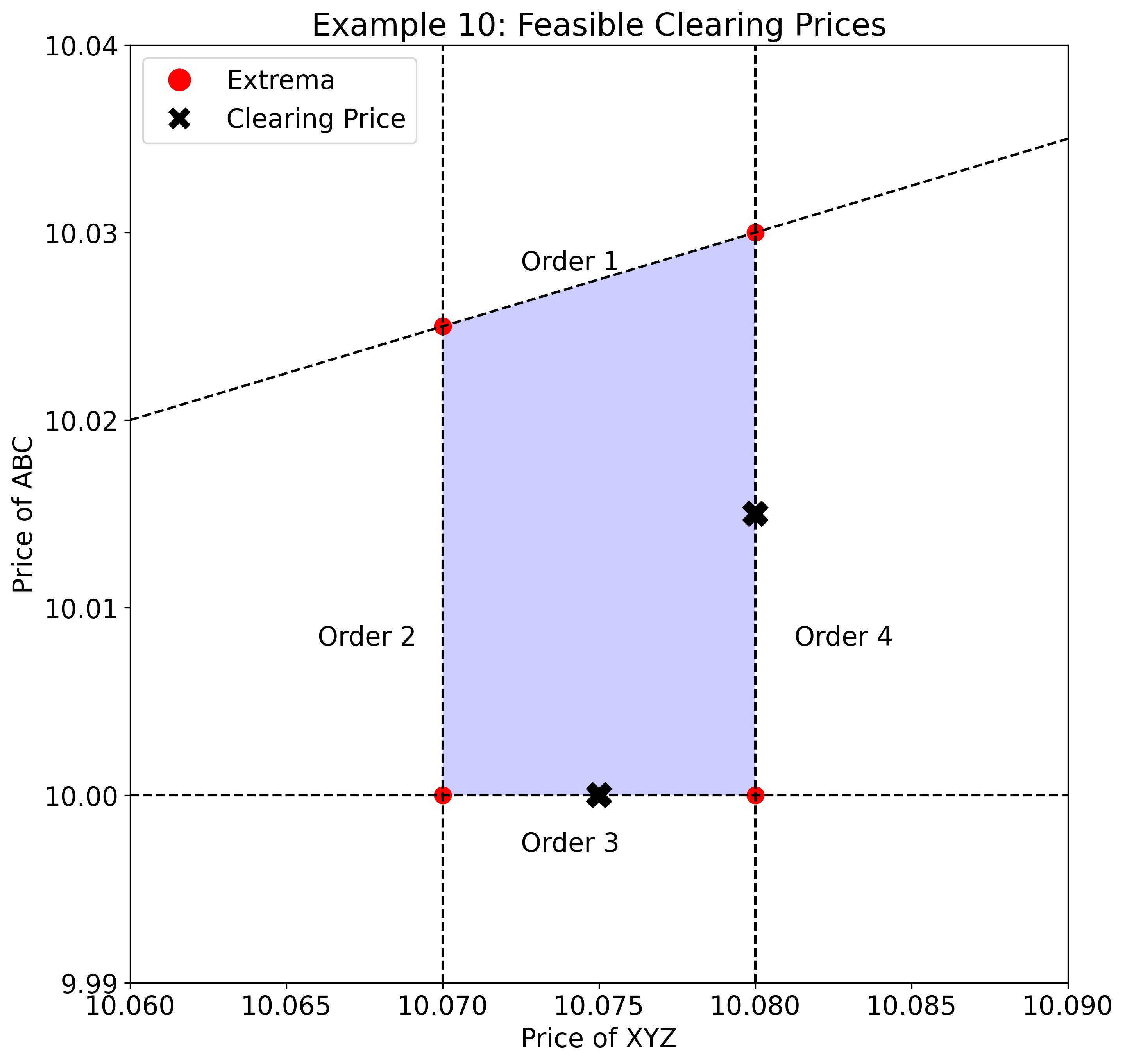
Example 10

Example 10: Scenario

• Order 1: Buy 200 ABC AND Sell 100 XYZ paying at most $998 net (Expressive Bidding constraint)
• Order 2: Sell 100 XYZ @ $10.07
• Order 3: Sell 200 ABC @ $10.00
• Order 4: Buy 200 XYZ @ $10.08

Example 10: Outcome

Order 1 fills 200 ABC @ $10.015 and 100 XYZ @ $10.075 resulting in a spread of $0.06. Order 2 fills @ $10.075. Order 3 fills @ $10.015. Order 4 fills @ $10.075.

Example 10: Key Takeaways

Order 1 results in the constraint $200\cdot p_\textrm{abc} - 100\cdot p_\textrm{xyz} \leq 998$. Order 2 introduces a new inequality into the system of equations from Example 9: $p_\textrm{xyz} \geq 10.07$. These constraints results in a clearing price range of $[\$10.07, \$10.08]$ with a midpoint of $10.075, and all orders receive price improvement.